HIPÉRBOLA
Una hipérbola es una sección cónica, una curva abierta de dos ramas obtenida cortando un cono recto por un plano oblicuo al eje de simetría, y con ángulo menor que el dela generatriz respecto del eje de revolución.
Es el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos llamados focos es constante.
Elementos de la hipérbola:
1Focos: Son los puntos fijos F y F'.
2Eje principal o real: Es la recta que pasa por los focos.
3Eje secundario o imaginario: Es la mediatriz del segmento FF'.
4Centro: Es el punto de intersección de los ejes.
5Vértices: Los puntos A y A' son los puntos de intersección de la hipérbola con el eje focal.
Los puntos B y B' se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio c.
Los puntos B y B' se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio c.
6Radios vectores: Son los segmentos que van desde un punto de la hipérbola a los focos: PF y PF'.
7Distancia focal: Es el segmento  de longitud 2c.
de longitud 2c.
8Eje mayor: Es el segmento  de longitud 2a.
de longitud 2a.
9Eje menor: Es el segmento  de longitud 2b.
de longitud 2b.
10Ejes de simetría: Son las rectas que contienen al eje real o al eje imaginario.
11Asíntotas: Son las rectas de ecuaciones: 
12Relación entre los semiejes: 
Ecuaciones de la hipérbola
Ecuaciones en coordenadas cartesianas: Ecuación de una hipérbola con centro en el origen de coordenadas 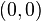 y ecuación de la hipérbola en su forma canónica.
y ecuación de la hipérbola en su forma canónica.
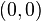 y ecuación de la hipérbola en su forma canónica.
y ecuación de la hipérbola en su forma canónica.
Ecuación de una hipérbola con centro en el punto 

Ejemplos:
a)
b)
Si el eje x es positivo, entonces la hipérbola es horizontal; si es al revés, es vertical. La excentricidad de una hipérbola siempre es mayor que uno.

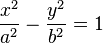
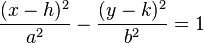




Comentarios
Publicar un comentario