TEOREMA FUNDAMENTAL DEL CÁLCULO
Primer teorema fundamental del cálculo
|
Usando la Regla de la cadena obtenemos como consecuencia directa del primer teorema fundamental del cálculo infinitesimal:
Siendo f(t) una función integrable sobre el intervalo [a(x),b(x)] con a(x) y b(x) derivables.
El segundo teorema fundamental del cálculo integral (o regla de Newton-Leibniz, o también regla de Barrow, en honor al matemático inglés Isaac Barrow, profesor de Isaac Newton) es una propiedad de las funciones continuas que permite calcular fácilmente el valor de la integral definida a partir de cualquiera de las primitivas de la función.
Enunciado
|
Demostración
Considere la siguiente primitiva de  definida en el intervalo
definida en el intervalo ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .:
.:
 definida en el intervalo
definida en el intervalo ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .:
.:-
-
 .
.
-
esto debido al primer teorema fundamental del cálculo el cual establece que:
-
-
![G'(x)=f(x) {\ } \forall x \in [a,b]](https://upload.wikimedia.org/math/c/1/c/c1c5b14eec3a07078372ecbb92a559e5.png) .
.
-
Como  y
y  son primitivas de
son primitivas de  , entonces
, entonces
 y
y  son primitivas de
son primitivas de  , entonces
, entonces-
-
![\exists C \in \mathbb{R}: {\ }G(x)=F(x)+C, {\ } \forall x \in [a,b]](https://upload.wikimedia.org/math/b/7/7/b7724a98dad3e4e2b5116f519cf5708c.png) .
.
-
Observe que
y de eso se sigue que 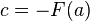 ; por lo tanto,
; por lo tanto,
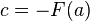 ; por lo tanto,
; por lo tanto,-
-
 .
.
-
Y en particular si 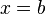 :
:
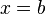 :
:Ejemplos

- DEFINICIÓN EN VÍDEO
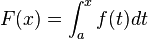 . Si f es continua en
. Si f es continua en  , entonces F es derivable en
, entonces F es derivable en  y F'(c) = f(c).
y F'(c) = f(c).



Comentarios
Publicar un comentario